Computer Networks Routing Algorithms Tool
Welcome to Our Interactive Learning Tool!
This is an educational interactive tool designed to help students better understand routing algorithms. With our tool, users can create a network and explore two distinct routing algorithms. Our user-friendly interface provides students with an improved visualization experience, allowing them to gain a deeper understanding of routing algorithm concepts.
Centralized Algorithm Explained
Centralized algorithms are algorithms that revolve around the starting node and create a coordinate system which maps the entire network. The mapping system defines all the nodes and all the edges in the network in relation to the starting node, and iterates through the lists of nodes and edges starting from the closest nodes to the starting node, until it reaches the end node.
Dijkstra's Algorithm
Dijkstra's Algorithm is a centralized Link-State algorithm used to find the path of shortest cost between two nodes and is widely used for network routing. It works by retreiving all the costs between the nodes on the network, putting them in lists and iteratively sorting and selecting the smallest cost that is connected to each node starting from the edges connected to the starting node and continuing from there. The algorithm updates a forwarding table, keeping a record of and printing the nodes previously used and the costs of the paths to connect them as it iterates closer to the last node. The table will be populated in order of nodes visited from the first node to the last node and will be the most cost-efficient path possible.
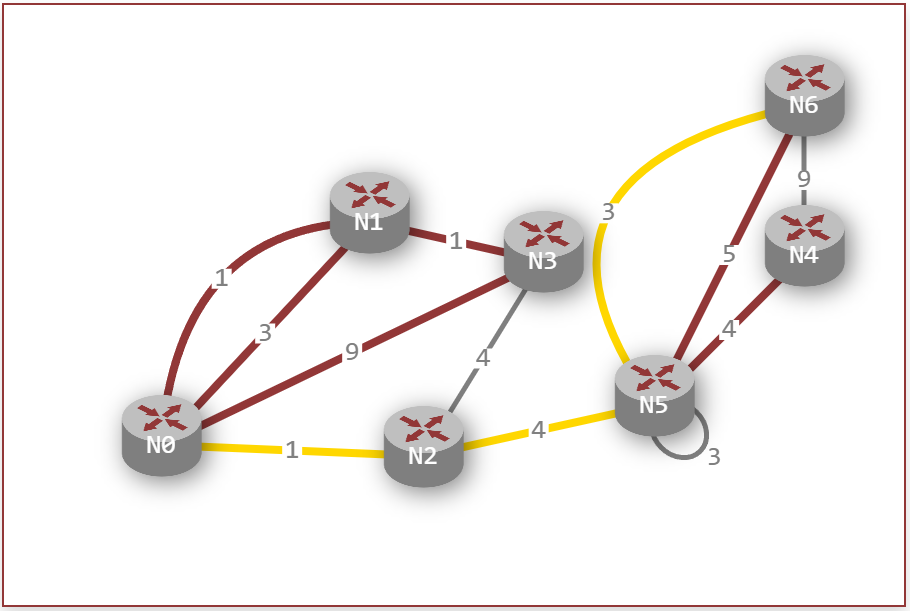
The step-by-step process goes as follows:
- Initialize the lists containing all the edges and the nodes connected to them, set the forwarding table distance from the starting node to 0, and set the rest to infinity for now.
- Iterate through, identify and select the least cost path connected to the starting node and add that value to the distance from the starting node. Mark down the node that the edge connects to as visited.
- Repeat the step above for the edges connecting to the last visited node and compare the nodes next to it. If a more cost-efficient path presents itself, the algorithm would back-track and redefine itself on that new path.
- This algorithm repeats the steps above until reaching the destination node, returning the final forwarding table.
To learn how to use this interactive learning tool, go to our Tutorial page.
Decentralized Algorithm Explained
Decentralized algorithms are algorithms that do not only revolve around the starting node but rather as a coordinate system where each node is responsible only for what edges connect it and the nodes communicate with each other using their local information to coordinate the most cost efficient route together to reach the end node starting from the starting node that is selected.
Bellman-Ford Algorithm
The Bellman-Ford Algorithm is a decentralized algorithm used to find the path of shortest cost between two nodes and is another type of algorithm used for network routing. It works by storing edge relations to each node, putting them in lists. Starting from the identified start node, the nodes communicate with each other, passing information about what the costs of its edges are and where they connect and through an iterative process coordinate the most cost-efficient path to the destination node. This algorithm also follows the same forwarding table rules as Dijkstra, marking down the nodes and costs associated as it routes from start to finish. Unlike Dijkstra, no back-tracking is done and in addition since Bellman-Ford follows a decentralized model it can handle negative edge costs as well. However, for the purpose of network routing there will not be any contexts that involve a negative edge cost.
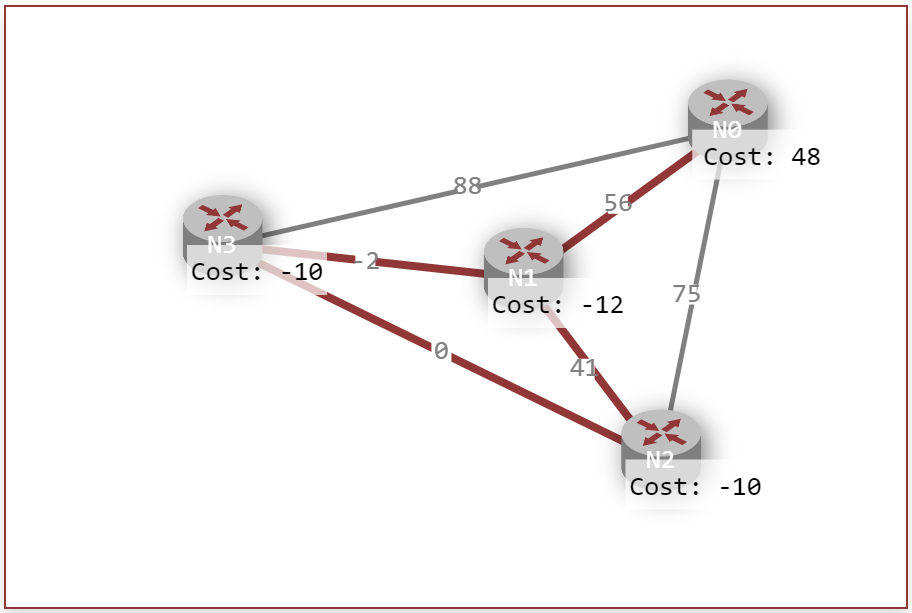
The step-by-step process goes as follows:
- Initialize the lists containing all the edges corresponding to each nodes connected to them and set the forwarding table distance from the starting node to 0 and the rest to infinity for now
- Iterate through all the edges of the first node, checking all possible paths to find the lowest cost path and once it is identified mark down the node the cost of the selected edge
- Go to the next node that connects to the other end of the previousy selected node and repeat the step above for the node you are currently on
- In the case of negative edges like the ones shown on the image above, the algorithm recognizes and works around it by ignoring as a possibility to choose it as the lowest cost edge connecting to the current node it is on
- This algorithm does the steps above until reaching the destination node, returning the final forwarding table
To learn how to use this interactive learning tool, go to our Tutorial page.